신경망 모델의 활성화 함수 기본 개념과 자주 사용되는 비선형 활성화 함수 Sigmoid, tanh, ReLU, LeakyReLU 특징과 활성화 함수 설정 가이드를 정리합니다.
활성화 함수의 역할과 특징

Activation function with respect to a single node 활성화 함수의 연산 과정을 하나의 node 뉴런에 대해서 정리하면 다음과 같다.
- Take Input and multiply by the neuron's weight ⇒ Add bias ⇒ Feed the result $x$ to the activation function $f(x)$ ⇒ Take the output and transmit to the next layer of neurons
- Output of Activation Function = f(input x weight + bias)
Activation Function 활성화 함수
Mathematical funtions that introduce non-linearity to a network.
- 활성화함수는 실제 데이터에 존재하는 비선형성과 같은 복잡한 패턴을 학습할 수 있도록 신경망 모델에 추가하는 함수이다.
- 뉴런의 input을 받아 가공 후 output을 다음 뉴런에 전달한다.
활성화 함수의 특징
Properties that Activation function should hold?
- Differential
Backpropagation 역전파 연산을 이용해 파라미터 weights & biase 를 업데이트 하기때문에 미분가능해야한다. - Monotonic function either entirely non-increasing or non-decreasing
Non-linear activation Functions
비선형 활성화 함수로 자주 사용되는 Sigmoid, Tanh, Relu, LeakyReLU, Softmax 를 정리해보자.
1. Sigmoid Function (Logistic Activation Function) 시그모이드 함수
신경망 분야에서 초창기부터 사용한 활성화 함수로, 임의의 실수값을 입력으로 받아 [0,1]사이의 범위로 압축해 출력하는 함수이다.

| Sigmoid Function | Output Range | Derivative |
|---|---|---|
| $f(x)=\sigma(x)=\frac{1}{1+e^{-x}}$ | $f(x) \in [0,1]$ | $f^{\prime}(x)=f(x)(1-f(x))$ |
- Activation function of Output layer for binary classification model : output을 확률로 압축하기 위해 최종 레이어의 활성화 함수로 시그모이드 함수를 많이 사용한다.
- Vanishing gradient problem 경사소실문제
- Not zero-centered Output Range : optimization harder : $[0,1]$ 모두 양의 값을 가지게되어 gradient updates go too far in different directions output.
- Slow convergence : 시그모이드 함수의 derivative function 그래프를 보면, 0과 가까울 때는 기울기가 크지만, 0에서 멀어질수록 (양 끝으로 갈수록) 기울기가 0에 가까워지며 매우 작아진다. 이는 파라미터를 업데이트하고 최적값에 수렴하는 속도 즉, 학습속도가 급격히 저하되는 문제가 존재한다.
2. Tanh
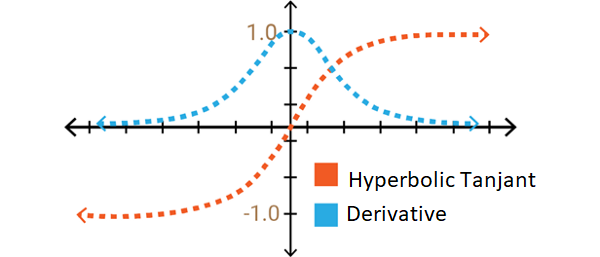
| Tanh Function | Output Range | Derivative |
|---|---|---|
| $f(x)=\tanh (x)=\frac{2}{1+e^{-2 x}}-1$ | $[-1,1]$ | $f^{\prime}(x)=1-f(x)^{2}$ |
- Scaled sigmoid function : $Tanh(x) = 2sigmoid(2x)-1$
- _Zero-centered Output Range : makes optimization easier 양,음의 값을 모두 가지게 되므로, 최적값에 수렴하는 것이 쉬워진다.
Vanishing Gradients & ReLU

3. Relu ( Rectified linear unit ) **

| Relu Function | Output Range | Derivative |
|---|---|---|
| $f(x) = max(x,0)=\left\{\begin{array}{l} 0 \text { for } x<0 \\ x \text { for } x \geq 0 \end{array}\right.$ | $f(x) \in [0,+ \infty]$ | $f^{\prime}(x)=\left\{\begin{array}{l} 0 \text { for } x<0 \\ 1 \text { for } x \geq 0 \end{array}\right.$ |
- Avoids Vanishing Gradient problem
- the default activation for hidden layers & Can only be used within hidden layer (output is not scaled)
- It does not activate all the neurons at the same time ⇒ Computationally efficient ⇒ Converge very fast
- It is said to have 6 times improvement in convergence from tanh function
- Some gradients are fragile during training and can die. It causes weight update which will make it never activate on any data point again.
- Dead ReLU : Problem of Dying neuron/Dead neuron due to Non-differentiable at zero
- the weighted sum for a ReLU unit ≥ 0 모든 0이상의 값에 대해서는 1의 값을 가지기 때문에, Vanishing/Exploding Neuron 문제가 해소된다.
- the weighted sum for a ReLU unit < 0 음수에 대해서는 0의 활성화 값을 출력해 역전파 연산이 멈출 수 있는 문제가 존재한다. 이러한 현상을 Dead ReLU unit 이라고 한다.
- Learning rate을 낮추는 것이 Dying ReLU를 막는데 도움이 될 수 있다.
4. Leaky ReLU
ReLU 함수의 Dead ReLU 문제를 해결하기 위해, constant slope 일정한 기울기를 추가한 함수이다.
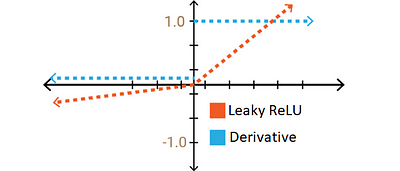
| Leaky ReLU Function | Output Range | Derivative |
|---|---|---|
| $f(x) =\left\{\begin{array}{l} \alpha x \text { for } x<0 \\ x \text { for } x \geq 0 \end{array}\right.$ | $[-\infty,+\infty]$ | $f^{\prime}(x)=\left\{\begin{array}{l} \alpha \text { for } x<0 \\ 1 \text { for } x \geq 0 \end{array}\right.$ |
5. SWISH (A Self-Gated Activation Function)
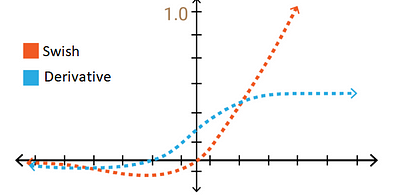
| SWISH (A Self-Gated Activation Function) | Range |
|---|---|
| $\sigma(x)=\frac{x}{1+e^{-x}}= x \times sigmoid(x)$ | $[-\infty,+\infty]$ |
Computer Science > Neural and Evolutionary Computing > Swish: a Self-Gated Activation Function
Tips for Activation Functions 💡
Activation Function Guideline
- Start with ReLU : As a rule of thumb, one can begin with using ReLU function and then move over to other activation functions in case ReLU doesn’t provide with optimum results
- ReLU는 일정 성능 이상을 보장하므로 ReLU로 설정하고 성능을 체크 (가장 많이 쓰임)
- 학습 중단 현상 ⇒ Dying ReLU 의심 ⇒ LeakyReLU 사용
- ReLU only for hidden layers 은닉층에서만 사용가능
- Tanh, Sigmoid : Vanishing gradient problem 발생 가능성 존재
- 얕은 신경망모델에서 사용
- Final output layer의 activation function으로 사용
- Sigmoid : 일반적으로 Classification 문제에서 잘 작동
- Batchnorm layer를 포함하는 신경망 모델의 경우, CNN layers - BatchNorm layer- Activation function 순서로 구성한다.
- Hyperparameters for Activation Functions : 프레임워크 디폴트값 사용
Reference&Source : Activation Functions by Himanshu S | Activation Functions in Neural Networks by akhi | Searching for Activation Functions
by Google Brain | ai-hub.kr/post/111/ |  | Activation Functions: A Short Summary |Comparison of Activation Functions for Deep Neural Networks
| Activation Functions: A Short Summary |Comparison of Activation Functions for Deep Neural Networks
'Certificate - DS > Deep learning specialization' 카테고리의 다른 글
| Model debugging and Loss curve (0) | 2021.11.23 |
|---|---|
| Hyperparameters Tuning 하이퍼파라미터 튜닝 (0) | 2021.11.22 |
| [Hyperparameters] Batch/Batch size/Epoch/Iteration 배치, 에포크 (0) | 2021.11.20 |
| Overfitting, Strategies to prevent overfitting 과적합과 과적합 문제를 해결하기 위한 방법 (0) | 2021.11.19 |
| [Optimization Algorithms] Gradient Descent (1) Batch, Stochastic, Mini-batch Gradient descent 배치, 확률적, 미니배치 경사하강법 (0) | 2021.11.19 |
